반응형
평균값(mean value, average value)
개념
-주기 T를 갖는 주기 파형의 전류 i(t)에 대하여 한 주기 동안의 평균값은 아래와 같이 정의됨

단일 펄스 파형의 평균값을 구하는 예

다중 펄스 파형의 평균값을 구하는 예

정류된 정현파의 평균값

실효값(effective value)
개념
*실효값 : 제곱(square)의 평균(mean)의 제곱근(root) → rms(root mean square)
-주기를 갖는 교류 전기에 의하여 일정 시간 동안 저항에서 발생되는 열의 정도를 A이라고하자
-이 때, 동일 시간 동안 A라는 열을 발생시키는 직류 전류나 직류 전압의 크기를 실효값이라 함

표현

실효값의 계산 방법
-정의식을 이용하여 계산하는 방법
-정의식과 파형의 성질을 이용하여 계산하는 방법
대칭성
-실효값은 파형의 순시값(instantaneous value)을 제곱한 것의 연산
*제곱을 하므로 절대값만이 의미가 있음
*따라서 한 주기 동안의 극성 변화와 무관
-실효값은 파형의 한 주기를 적분구간으로 갖는 정적분
*적분의 시점과 종점을 바꾸어도 그 결과가 같음 → 즉 i(t)와 i(-t)의 실효값은 같음

반파대칭(half-wave symmetry)

1/4파 대칭(quarter-wave symmetry)

펄스형 파형의 실효값
-단일 펄스 파형

-다중 펄스 파형

파형의 분해와 실효값의 계산
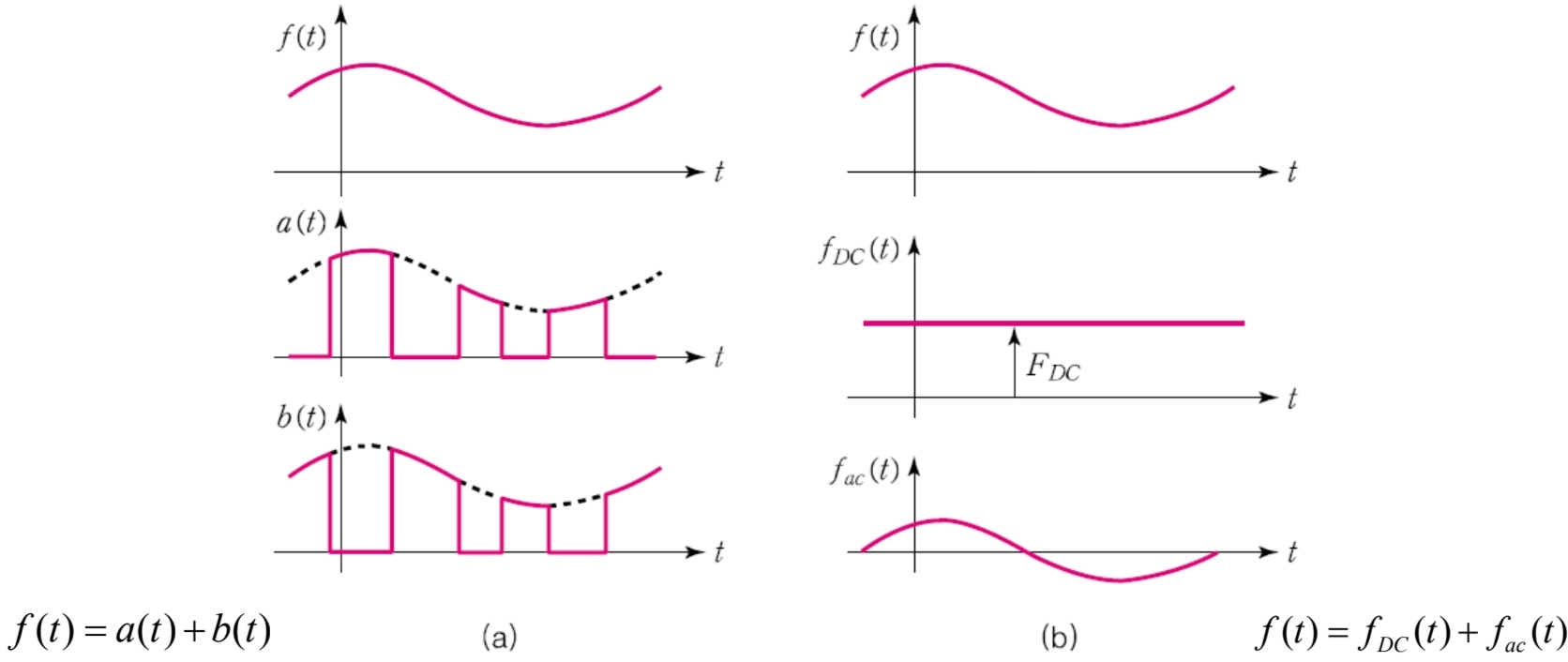
 |
 |
'전생했더니 전력전자였던 건에 대하여' 카테고리의 다른 글
| 2.3장_전력전자공학의 기초(인덕터와 커패시터) (0) | 2024.01.17 |
|---|---|
| 2.1장_전력전자공학의 기초 (0) | 2024.01.16 |
| 1.2장_기본(반도체의 기초) (1) | 2024.01.08 |
| 1.1장_기본(직류와 교류) (2) | 2024.01.07 |
| 0장_전력전자를 시작하며 (1) | 2024.01.07 |



